Confidence Interval on Linear Combination of Means, Independent Groups (1 of 5)

---

Following the general formula for a confidence interval, the formula for a confidence interval on a linear combination of means is:

L ± t s_L

where L is the linear combination of the sample means, t depends on the level of confidence desired and the degrees of freedom, and S_L is an estimate of σ_L, the standard error of a linear combination of means.

The formula for S_L is:



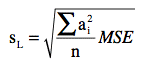
which is the same as the formula for σ_L except that MSE (an estimate of σ²) is used in place of σ². The formula for MSE here is very similar to the formula for MSE used in the calculation of a confidence interval on the difference between two means. The formula is:



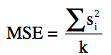
where is the sample variance of the ith group and k is the number of groups. This formula assumes homogeneity of variance and that the k sample sizes are equal.