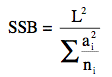Orthogonal Comparisons (4 of 5)

next previous
If a set of a-1 orthogonal comparisons is constructed and the sum of squares for each comparison is computed, then the sum of the a-1 sums of squares will be equal to the sum of squares between in the one factor analysis of variance. For example, consider the data described in the section on partitioning the sums of squares. The means for the three groups are:

M1 = 4
M2 = 3
M3 = 2,
n = 4, and,
as previously computed, SSB = 8.

The SSB can also be computed by making up two orthogonal comparisons among the three means and adding the sums of squares associated with each. A set of orthogonal comparisons is: 
Mean 1    2   0
Mean 2   -1   1
Mean 3   -1  -1

The formula for each sum of square is:


next previous