Confidence Interval for μ, Standard Deviation Known (3 of 3)
Next section: Mean, σ estimated
Therefore, 468.02 ≤ μ ≤ 591.98. Naturally, if a larger sample size had been used, the range of scores would have been smaller.
The computation of the 99% confidence interval is exactly the same except that 2.58 rather than 1.96 is used for z. The 99% confidence interval is: 448.54 ≤ μ ≤ 611.46. As it must be, the 99% confidence interval is even wider than the 95% confidence interval.
Summary of Computations
- Compute M = ΣX/N.
- Compute
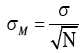
- Find z (1.96 for 95% interval; 2.58 for 99% interval)
- Lower limit = M - z σM
- Upper limit = M + z σM
- Lower limit ≤ μ ≤ Upper
limit
Assumptions:
- Normal distribution
- σ is known
- Scores are sampled randomly and are independent
Next section: Mean, σ estimated