Area Under a Portion of the Normal Curve (1 of 4)

---

If a test is normally distributed with a mean of 60 and a standard deviation of 10, what proportion of the scores is above 85? This problem is very similar to figuring out the percentile rank of a person scoring 85. The first step is to figure out the proportion of scores less than or equal to 85. This is done by figuring out how many standard deviations above the mean 85 is. Since 85 is 85-60 = 25 points above the mean and since the standard deviation is 10, a score of 85 is 25/10 = 2.5 standard deviations above the mean. Or, in terms of the formula,

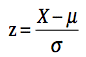= (85-60)/10 = 2.5

A z table can be used to calculate that 0.9938 of the scores are less than or equal to a score 2.5 standard deviations above the mean. It follows that only 1-0.9938 = .0062 of the scores are above a score 2.5 standard deviations above the mean. Therefore, only 0.0062 of the scores are above 85.