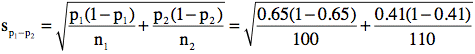Confidence Interval on the Difference Between Proportions (3 of 4)
Finally, the value of z for the 99% confidence interval is computed using a z table; it is 2.58. The lower limit of the confidence interval is simply:
p1 - p2 - (z) (estimated
)= 0.65 - 0.41 - (2.58)(0.067) = 0.07
The upper limit is:
= 0.65 - 0.41 + (2.58)(0.067) =0.41
The 99% confidence interval is therefore:
0.07 ≤ π1 - π2 ≤ 0.41.
This indicates that the proportion of psychology majors that can solve the problem is from 0.07 to 0.41 higher than the proportion of physics majors that can solve it.
Summary of Computations
-
Compute p1 - p2.
- Find z for confidence interval using a z
table.
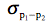- with the formula:
