Confidence Interval, Difference between Independent Correlations (2 of 4)
The problem is to construct the 95% confidence on the difference between correlations.
The formula is:
The first step is to use the r to z' table to convert the two r's. The r of 0.55 corresponds to a z' of 0.62 and the r of 0.42 corresponds to a z' of 0.45. Therefore,
The next step is to find z. From a z table, it can be determined that the z for 95% confidence intervals is 1.96. Finally,
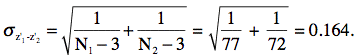
Therefore,
Lower limit = 0.17 - (1.96)(0.164) = -0.15
Upper limit = 0.17 + (1.96)(0.164) = 0.49
Converting the lower and upper limits back to r, results in r's of -0.15 and 0.45 respectively. Therefore, the confidence interval is:
-0.15 ≤ ρ1 - ρ2 ≤ 0.45
where ρ1 is the population correlation for females and ρ2 is the population correlation for males.