One- and Two-Tailed Tests (1 of 4)
In the section on "Steps in hypothesis testing" the fourth step involves calculating the probability that a statistic would differ as much or more from parameter specified in the null hypothesis as does the statistic obtained in the experiment. This statement implies that a difference in either direction would be counted. That is, if the null hypothesis were:
H0: μ- μ = 0
and the value of the statistic M1- M2 were +5, then the probability of M1- M2 differing from zero by five or more (in either direction) would be computed. In other words, probability value would be the probability that either M1- M2 ≥ 5 or M1- M2 ≤ -5.
Assume that the figure shown below is the sampling distribution of M1- M2.
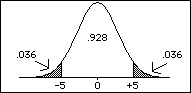
The figure shows that the probability of a value of +5 or more is 0.036 and that the probability of a value of -5 or less is .036. Therefore the probability of a value either greater than or equal to +5 or less than or equal to -5 is 0.036 + 0.036 = 0.072.