Confidence Interval on Linear Combination of Means, Independent Groups (5 of 5)

---

Next section: Pearson's correlation

Summary of Computations

1. Compute the sample mean (M) for each group.
   
   
2. Compute the sample variance (s²) for each of the k groups.
   
   
3. Find the coefficients (a's) so that Σ a_iμ_i is the parameter to be estimated.
   
   
4. Compute L = a₁M₁ + a₂M₂ + ... + a_kM_k
   
   
5. Compute MSE = Σs² /k
   
   
6. Compute
   
   
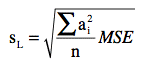
7. Compute df = k(n-1) where k is the number of groups and n is the number of subjects in each group.
   
   
8. Find t for the df and level of confidence desired using a t table
   
   
9. Lower limit = L - t s_L
   
   
10. Upper limit = L + t SL
    
    
11. Lower limit ≤ Σa_iμ_i ≤ Upper limit
    

Assumptions:

1. All populations are normally distributed.
   
   
2. All population variances are equal (homogeneity of variance)
   
   
3. Scores are sampled randomly and independently from k different populations.
   
   
4. The sample sizes are equal.
   

Next section: Pearson's correlation