Area Under a Portion of the Normal Curve (4 of 4)

previous


Assume a test is normally distributed with a mean of 100 and a standard deviation of 15. What proportion of the scores would be between 85 and 105? The solution to this problem is similar to the solution to the last one. The first step is to calculate the proportion of scores below 85. Next, calculate the proportion of scores below 105. Finally, subtract the first result from the second to find the proportion scoring between 85 and 105.

Begin by calculating the proportion below 85. You can caluclate that 85 is one standard deviation below the mean:

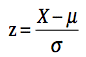z formula = (85 - 100)/15 = -1

Using a z table with the value of -1 for z, the area below -1 (or 85 in terms of the raw scores) is 0.1587.

Doing the same thing for 105,

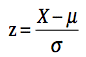z formula = (105 - 100)/15 = 0.333

A z table shows that the proportion scoring below 0.333 (105 in raw scores) is .6306. The difference is .6306 - .1587 = .4719. So, .472 of the scores are between 85 and 105.

normal distribution showing areas



previous