Conditional Probability



A conditional probability is the probability of an event given that another event has occurred. For example, what is the probability that the total of two dice will be greater than 8 given that the first die is a 6? This can be computed by considering only outcomes for which the first die is a 6. Then, determine the proportion of these outcomes that total more than 8. All the possible outcomes for two dice are shown below:

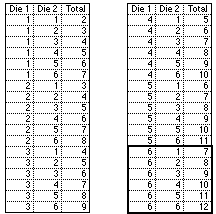
all outcomes two dice

There are 6 outcomes for which the first die is a 6, and of these, there are four that total more than 8 (6,3; 6,4; 6,5; 6,6). The probability of a total greater than 8 given that the first die is 6 is therefore 4/6 = 2/3.

More formally, this probability can be written as:

p(total>8 | Die 1 = 6) = 2/3.

In this equation, the expression to the left of the vertical bar represents the event and the expression to the right of the vertical bar represents the condition. Thus it would be read as "The probability that the total is greater than 8 given that Die 1 is 6 is 2/3." In more abstract form, p(A|B) is the probability of event A given that event B occurred.